The rhombus, which we are familiar with from geometry lessons, has always been one of the challenging subjects in terms of its features. On the contrary, we answered in the simplest form by which formulas the area of a rhombus is calculated, how many degrees are its interior angles, and what properties it has.
GeometryAlthough it is a course that is disliked by many students, it is one of the most important parts of our daily lives. It is derived from the Greek words “Geo” (earth) and “Metro” (measurement). The famous historian and writer Herodotus said that although geometry is not certain, its origin was Egypt.
The subject of this article is geometry, which is one of the important parts of geometry. equilateral quadrangle. This shape, also known as diamond, has many important features. Let’s learn more about rhombus properties, area calculation formulas and interior angles.
What is a rhombus?
Equilateral quadrangleis a special case of a parallelogram. Opposite sides in a rhombus are parallel to each other and opposite angles are equal, thus satisfying the conditions of a parallelogram. Also, all the sides of the rhombus are equal in length and the diagonals intersect each other at right angles. A rhombus has all its angles 90 degrees If so, it can also be called a square.
In the figure above, AB, BC, CD and AD are sides of rhombus and you can see a rhombus ABCD where AC and BD are the diagonals of the rhombus.
Is a square a rhombus?
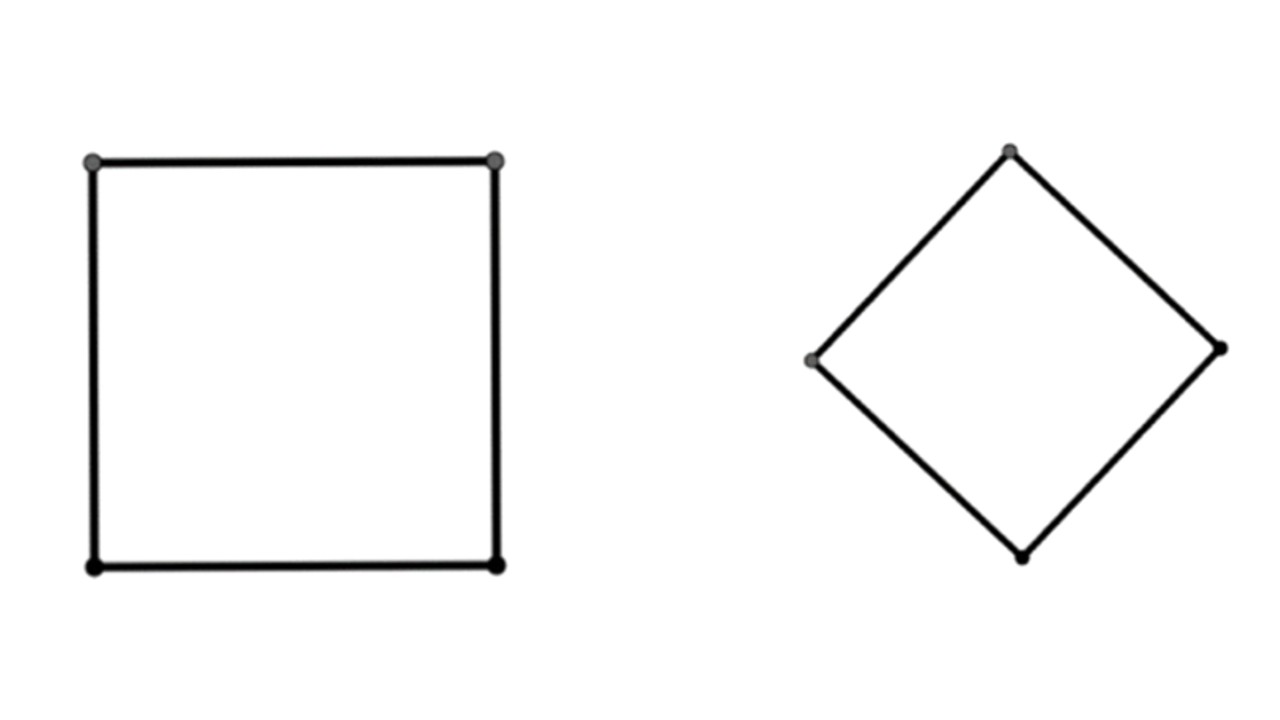
square and equilateral quadrangle has some similarities and differences. Both rhombus and square have similar properties as they are also called parallelograms. In a rhombus, one pair of opposite angles in the rhombus are acute and the other pair of angles are obtuse. However, this is different in the case of a square because each of the four angles is 90 degrees.
Since all sides of a square are equal in length, a square is always equilateral quadrangle can be counted as. In addition, the diagonals of both the square and the rhombus are perpendicular to each other and bisect opposite angles. So a square can always also be called a rhombus.
How to calculate the area of a rhombus?
- Method #1: Calculate area using diagonals
- Method #2: Calculating area using base and height
- Method #3: Calculating area using trigonometry (i.e. using sides and angles)
Method #1: Calculate area using diagonals (A = (d 1 × d 2 ) / 2)
- Step #1: An ABCD with two diagonals AC and BD rhombus Let’s take it.
- Step #2: Find the length of a diagonal, So d1 is the distance between A and C.
- Step #3: Find the length of its two diagonals, that is, d2, which is the distance between B and D.
- Step #4: Multiply both diagonals d1 and d2.
- Step #5: Divide the result by 2.
- Step #6: The result will give the area of rhombus ABCD.
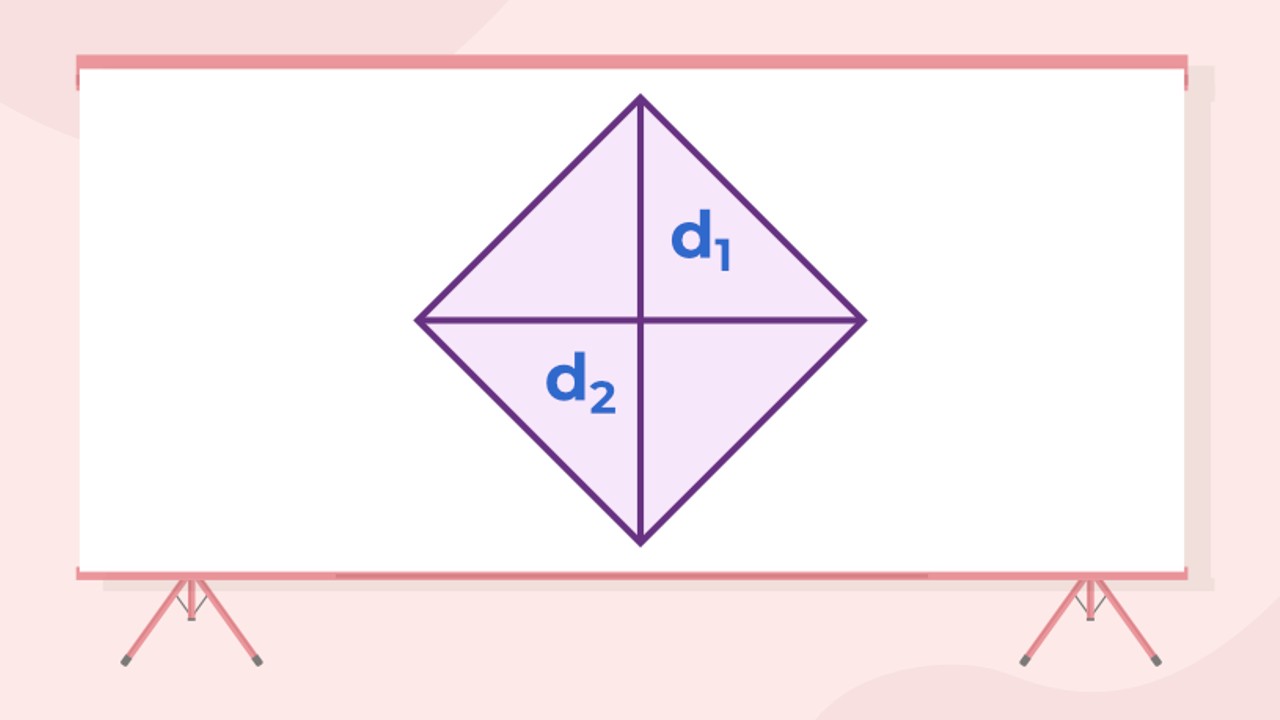
Just follow the steps above to calculate the area of a rhombus using the diagonal lengths. Although it is a little longer than other calculation methods, it is one of the most frequently used methods.
Area calculation sample question and solution using diagonals:
Example question:
Calculate the area of a rhombus whose diagonals are 6 cm and 8 cm.
Solution:
d1 = 6cm
d2 = 8cm
Area of rhombus, A = (d 1 × d 2 ) / 2
= (6 × 8) / 2
= 48 / 2
= 24 cm2
Therefore, the area of the rhombus is 24 cm².
Method #2: Calculate area using base and height (A = b × h)
- Step #1: rhombus Find and calculate the base and height values from the given figure.
- Step #2: Multiply the base and the calculated height.
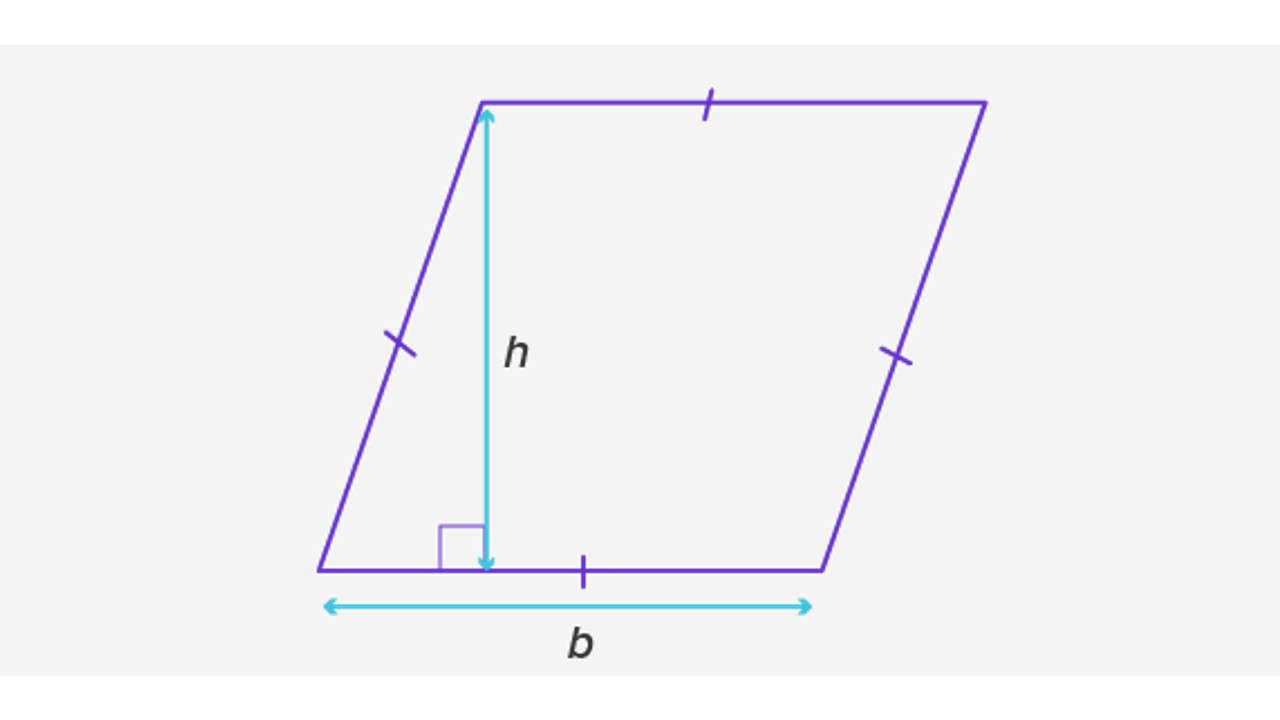
You can use the base and height along with the steps above to calculate the area of the rhombus.
Area calculation sample question and solution using base and height:
Example question:
Calculate the area of a rhombus with a base of 10 cm and a height of 7 cm.
Solution:
Base, b = 10 cm
Height, h = 7cm
Area, A = b × h
= 10 × 7 cm²
A = 70 cm²
Method #3: Calculate area using trigonometry (A = s² × sin (30°))
- My name #one: Square the length of any of the sides of the rhombus.
- My name #2: Multiply by the sine of one of the angles.
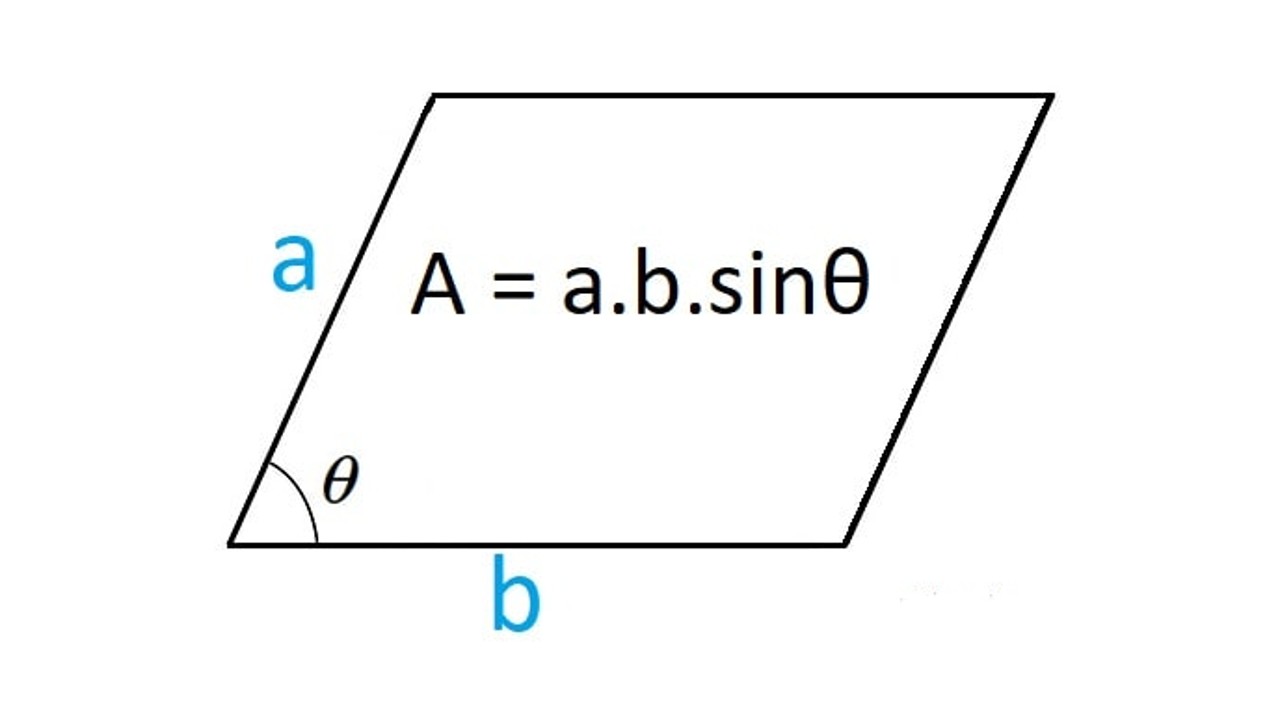
It is one of the least preferred methods for calculating the area of a rhombus. By following the steps above, you can calculate trigonometric area.
Area calculation sample question and solution using trigonometry:
Example question:
Calculate the area of a rhombus whose side length is 2 cm and one of the angles A is 30 degrees.
Solution:
Side = s = 2cm
Angle A = 30 degrees
Side length squared = 2 × 2 = 4
Area, A = s² × sin (30°)
A = 4 × 1/2
A = 2 cm²
Properties of rhombus:
- Opposite angles are equal to each other
- They are called by three different names
- Diagonals bisect each other at 90 degrees
- The sum of the interior angles is 360.
Opposite angles are equal to each other
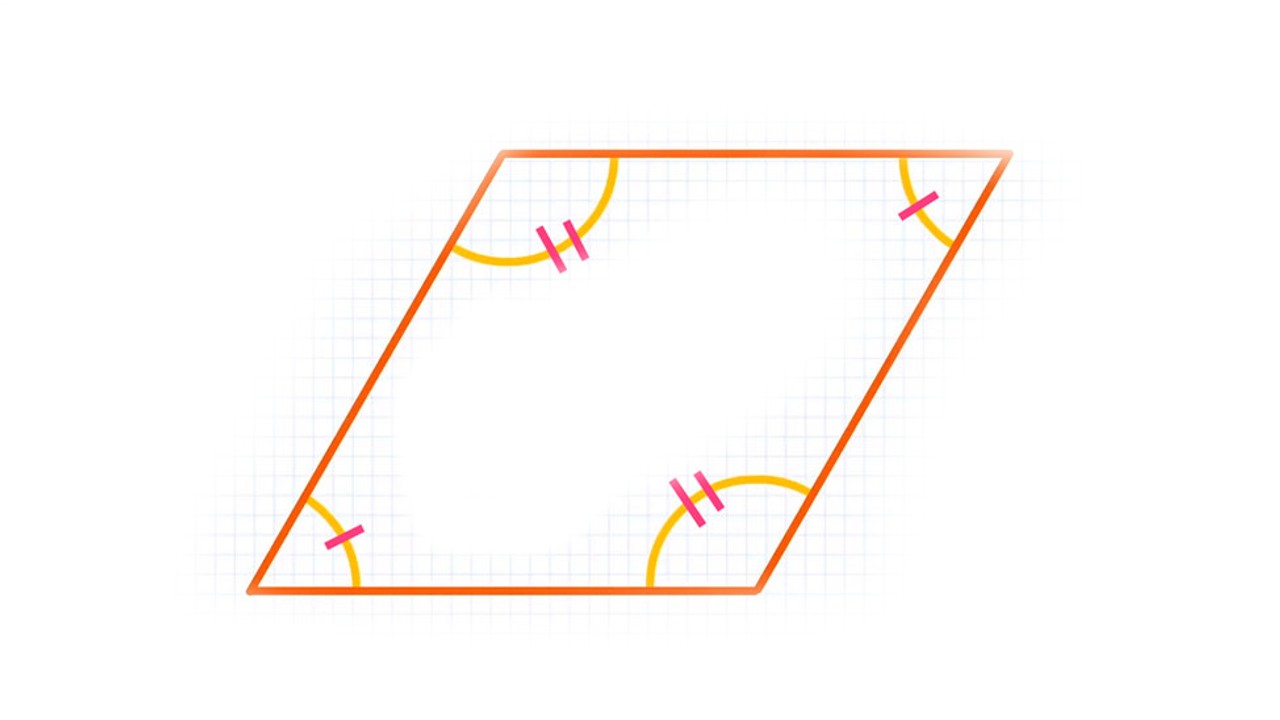
rhombus As its name suggests, it has four interior angles. You can also create two diagonals inside a rhombus by connecting opposite corners. No matter how you arrange this shape on a flat surface, it will always two equal opposite angles You’ll see that you have it.
They are called by three different names
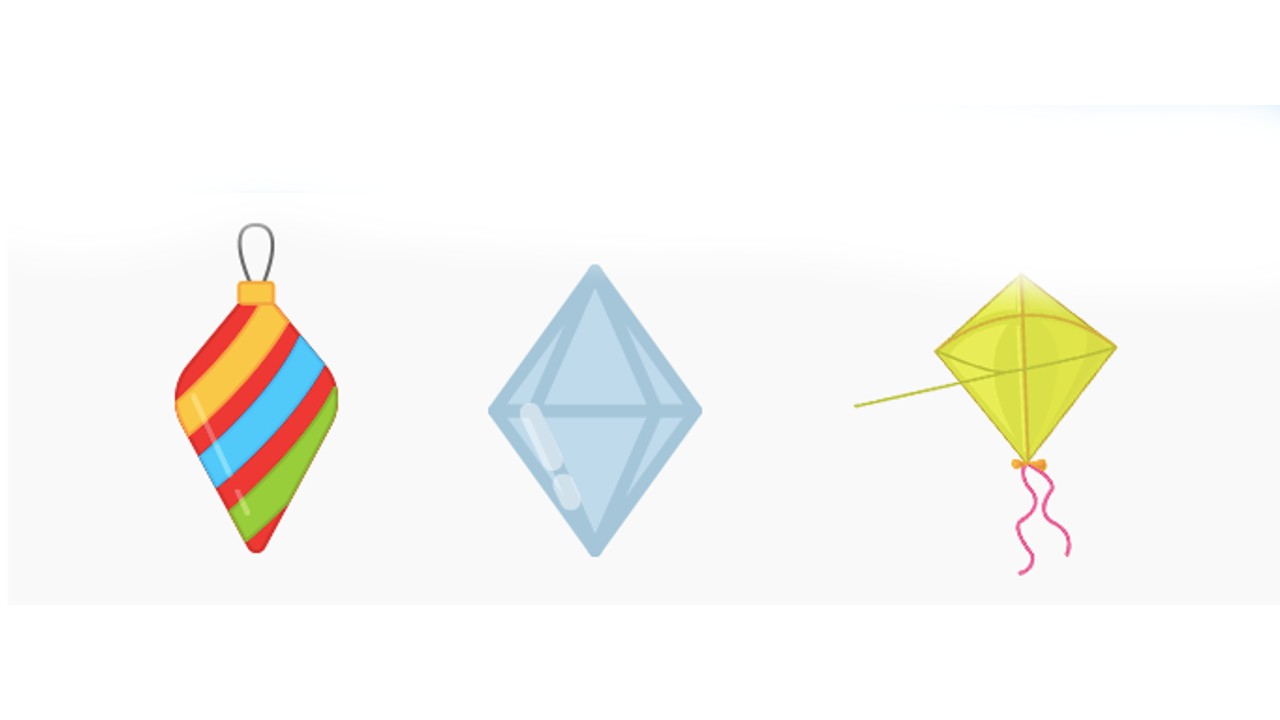
Equilateral quadrangleIn terms of its appearance, it resembles many objects we may encounter in our daily lives. However, they are generally referred to by three different names.
- Equilateral quadrangle
- Lozenge
- Diamond
Diagonals bisect each other at 90 degrees
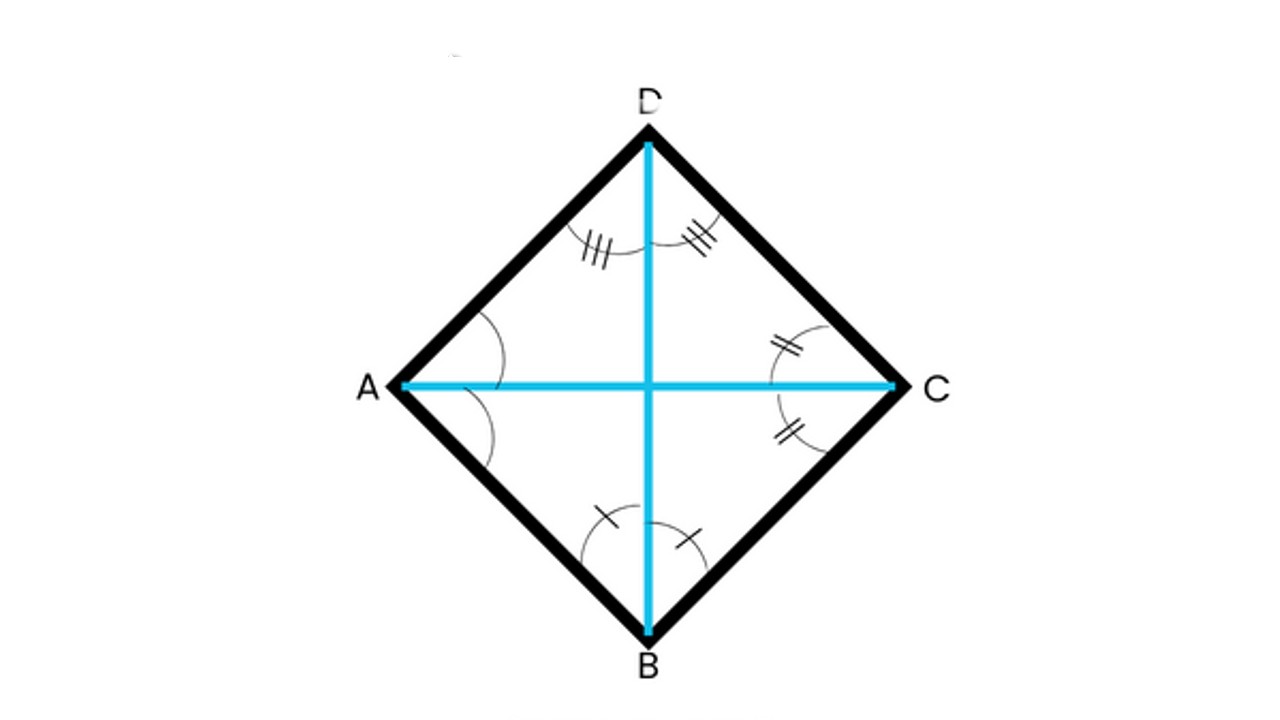
rhombus Another interesting and wonderful feature is that its diagonals are always perpendicular to each other. No matter what interior angles it has, the diagonals of a rhombus are always at right angles to each other. At the same time, these diagonals divide each other into exactly two equal parts.
The sum of the interior angles is 360 degrees
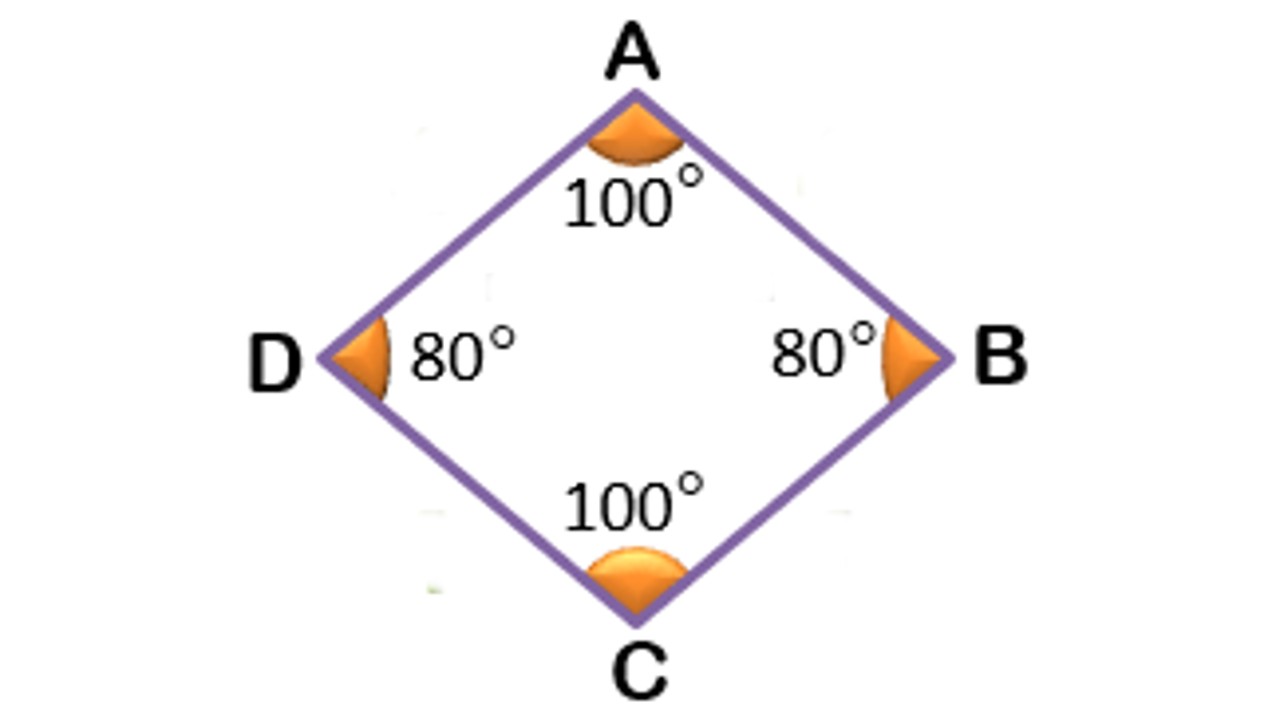
As we mentioned above, it is also considered a special case of parallelogram. rhombus its diagonals divide it into 2 triangles. As you know, the sum of the interior angles of a triangle is 180 degrees. In other words, since 2 triangles are formed, the sum of the interior angles is 360 degrees We can see that it is.
