How to Calculate the Volume of the Sphere, What is the Formula?

Even though most of us have seen mathematics and geometry lessons in our last high school years, we are constantly encountering them in our daily lives without realizing it. Geometric shapes are already actively used in many business areas such as engineering. One of them is the sphere. The sphere looks like a simple round when viewed from the outside. but it is one of the most important geometric shapes with perfect symmetry.

Since it is not easy to find the volume, area and similar measurements of the sphere, there is a special formula you need to use. After knowing this formula, it is possible to find the volume of the sphere with a few simple operations by placing the necessary variables in their places. Of course, in more complex operations, the volume of the sphere may only be the first step to the solution. Bride How to find the volume of a sphere Let’s take a closer look at the question and see the formula you need to use for this calculation.

For those who don’t know, what is a sphere?

A sphere is a geometric shape defined as symmetrically perfect. The sphere, which is also a surface, exists in three-dimensional Euclidean space. Even though we think it’s the same in everyday life In fact, in mathematics and geometry, solid and hollow spheres are evaluated separately. A filled sphere is called a round. The hollow sphere is two-dimensional while the round is three-dimensional. A one-dimensional sphere is a circle.

Here is the special formula you should use to calculate the volume of the sphere:

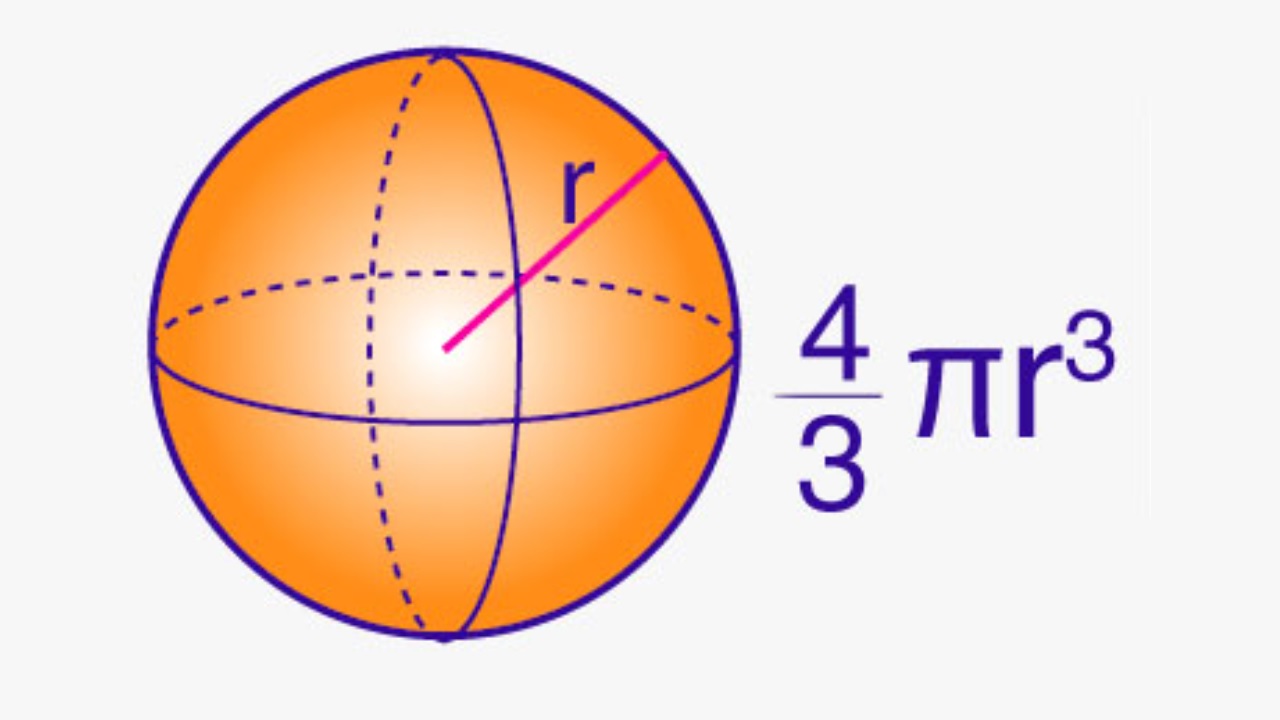
We will go into details while explaining it through an example, but first, let’s write the formula that you need to use for this process, which is the most basic answer to the question of how to measure the volume of the sphere. The volume calculation formula for the sphere is V = ⁴⁄₃πr³. Write down this formula immediately and if the pen and paper are ready, start examining our example immediately.

How is the volume of a sphere calculated? Let’s explain through an example:

• Step #1: Write down the volume calculation formula of the sphere in a corner.
• Step #2: First find the radius and substitute it in the formula.
• Step #3: Find the cube of the radius and substitute it in the formula.
• Step #4: Multiply the radius you cubed by the value in the formula.
• Step #5: Finally, multiply the value you get by the number of pi.

Step #1: Write down the volume calculation formula for the sphere:

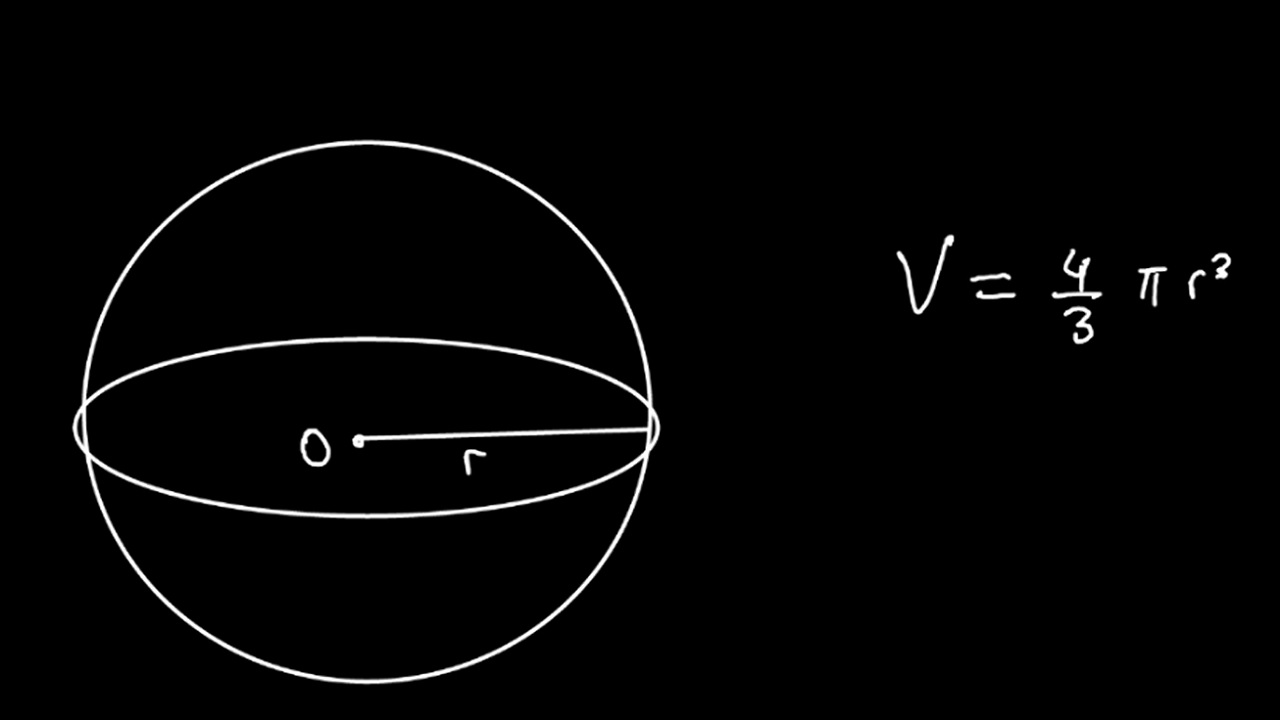
As we mentioned above, the volume calculation formula for the sphere is V = ⁴⁄₃πr³. If you are not a master mathematician and if you are not going to do all the operations in your mind, you should first write this formula down in a corner. You will have to perform the next steps on the formula V = ⁴⁄₃πr³ anyway. In the formula, V represents the volume of the sphere and r represents the radius of the sphere.

Step #2: First find the radius and replace it in the formula:

In order to calculate the volume of the sphere, it is necessary to find the radius of the sphere, that is, the r value. In some questions, the radius of the sphere can be given directly. If this is the case, you can proceed to the next step. If the radius of the sphere is not given, all you have to do is divide the diameter of the sphere in half. For this example, let’s take the radius of the sphere as 1 cm.

Let’s open a parenthesis at this point. In some questions, the surface area of ​​the sphere is given instead of the diameter or radius. In such a case, do not worry and find the radius of the sphere by applying the formula; r = square root ( surface area / 4π )

Step #3: Find the cube of the radius and substitute it in the formula:

Now that we have found the radius of the sphere, We need to cube the radius of the sphere. This value, which is shown as r³, can be found as rxrxr. Since the radius in our example is 1, 1 x 1 x 1 = 1, that is, r³ = 1. Substituting this value in the formula, the following table appears; V = ⁴⁄₃π x 1

In this example, it is not confusing that we give the radius of the sphere as 1 for easy understanding. Where the radius of the sphere is 2 The result is 2 x 2 x 2 = 8, so r³ = 8. With some large numbers, the result may be large, but always write in cm.

Step #4: Multiply your cubed radius by the value in the formula:

After finding the cube value of the radius of the sphere as 1, write it down in the formula. It turned into a process of V = ⁴⁄₃π x 1. The first thing you need to do at this point is to multiply r³, that is, 1 by 4/3. 4/3 x 1 = 4/3. When we put it in the formula, we see a table in the form of V = ⁴⁄₃π.

Step #5: Multiply your final value by the number of pi:

We found the radius of the sphere, calculated its cube and multiplied by the value 4/3 as in the formula. Now it’s time as in the formula V = ⁴⁄₃π the last step is to multiply by the number pi. In such operations, the pi number is included in the formula as 3.14 unless otherwise stated. So V = ( 3.14) x 4/3 which is V = 4.19. Since we have determined all these operations as cubic units, the volume of the sphere, V = 4.19 cm3

Things to consider when calculating the volume of the sphere:

• Make sure that all the units you operate on the formula are the same. So use all numbers in meters or centimeters.
• Since the sphere is a shape in Euclidean space, all units must be cubic in the form of m³.
• If the process asks you for half or a quarter of the sphere volume, still find the entire volume first and then multiply it by ½ for half the value and ¼ for the quarter.

Here are some of the other formulas you can use in sphere operations:

• Projection area of ​​the sphere: APF = 4/3πr²
• Part volume of the sphere: VKS = h²π / 3 ( 3r – h )
• Moment of inertia of the sphere: J = 2 / 5 x mr²
• Surface area of ​​the sphere: A = 4πr² = d²π

It has the perfect symmetry that we encounter in mathematics and geometry. Answering the question of how to calculate the volume of a sphere We shared the formula you can use for the calculation process. Of course, the sphere is an extremely complex subject, but in this article, we aimed to provide general information for those who do not know.